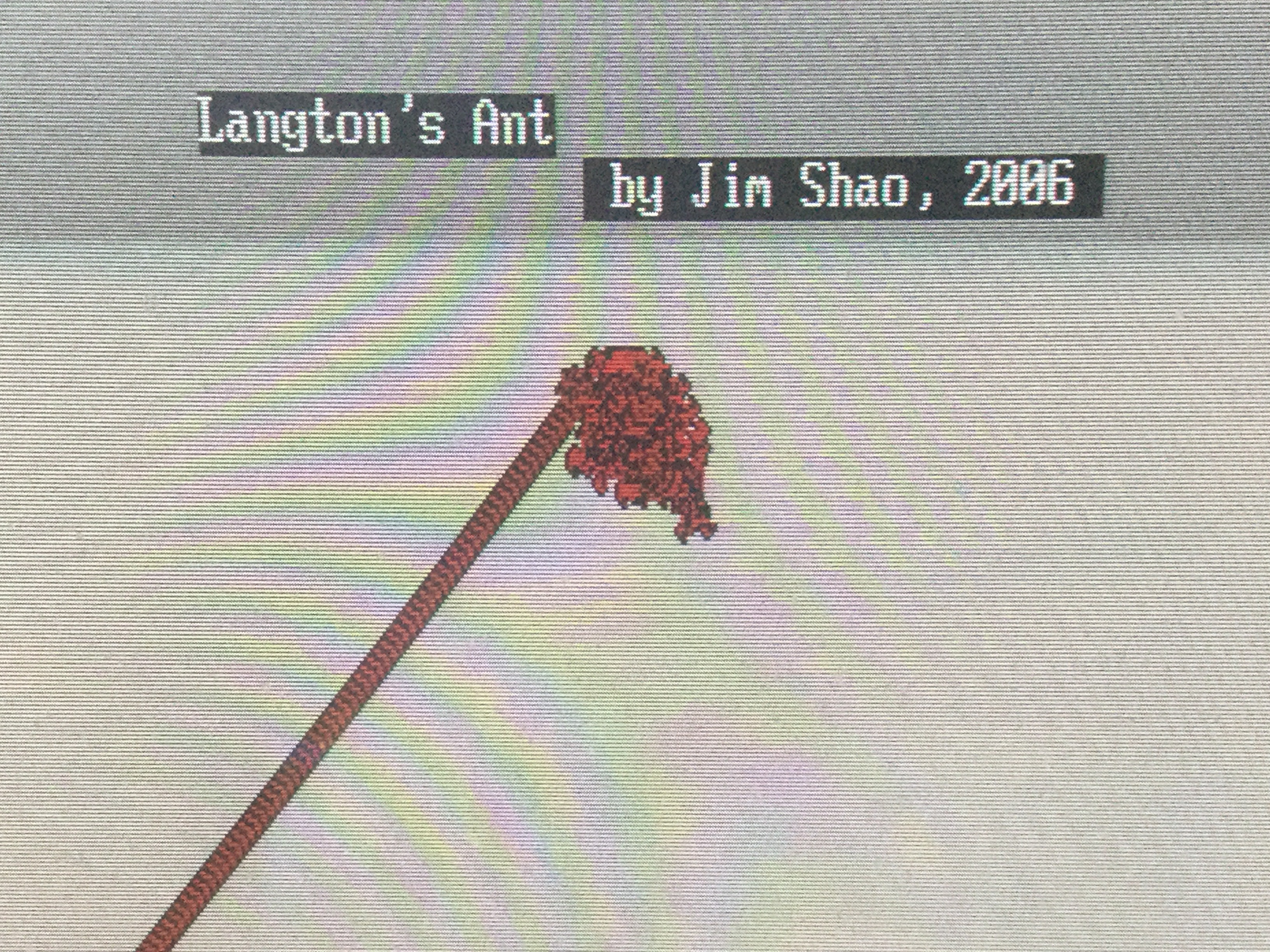
照片1:原始条件下的兰顿氏蚁行结果。
小 鹰
兰顿氏蚁(Langton's ant)是克里斯托弗·兰顿[1]於1986年创造的一个二维四态的图灵(Alan M. Turing)机。
操作规则如下:将一虚拟蚂蚁置于底色全白的棋盘方阵上,
一,若蚂蚁所在方格为黑色,该蚁左转90度,进入邻接的方格;
二,若蚂蚁所在方格为白(或红)色,该蚁右转90度,进入邻接的方格;
三,在进入下一方格之前,该蚁须将原来所在方格从黑色改为红色,或从白(或红)色改为黑色。
按此规则连续运作的结果显示,经过一万多步混沌式的漫游,该蚁终於开始建造一条104步宽的“高速公路”(“highway”, or a periodic motion with drift),朝一定方向无限延伸,直到受到干扰为止。
2006年,我出於好奇和自娱,按此规则编写了个计算机程序,重复了兰顿的结果。(见照片1)

照片1:原始条件下的兰顿氏蚁行结果。
然后,我稍微改变一下初始条件,例如,预先改换一个紧邻起始点方格的底色,结果,蚂蚁的行径“大相径庭”,虽然最终牠也建造了另一条“高速公路”。(见照片2)

照片2:初始条件稍有改变后的兰顿氏蚁行结果。
进而,我又在兰顿氏蚁的路径上预先随机地改变方格的底色,想看看这只因干扰而迷失方向的蚂蚁会如何表现?结果显示,接连十次受到微扰的兰顿氏蚁,或迟或早,总是能够“顽强”地重建自己的“高速公路”,只是新路与旧路的方向夹角为零度、70度或110度。(见照片3)
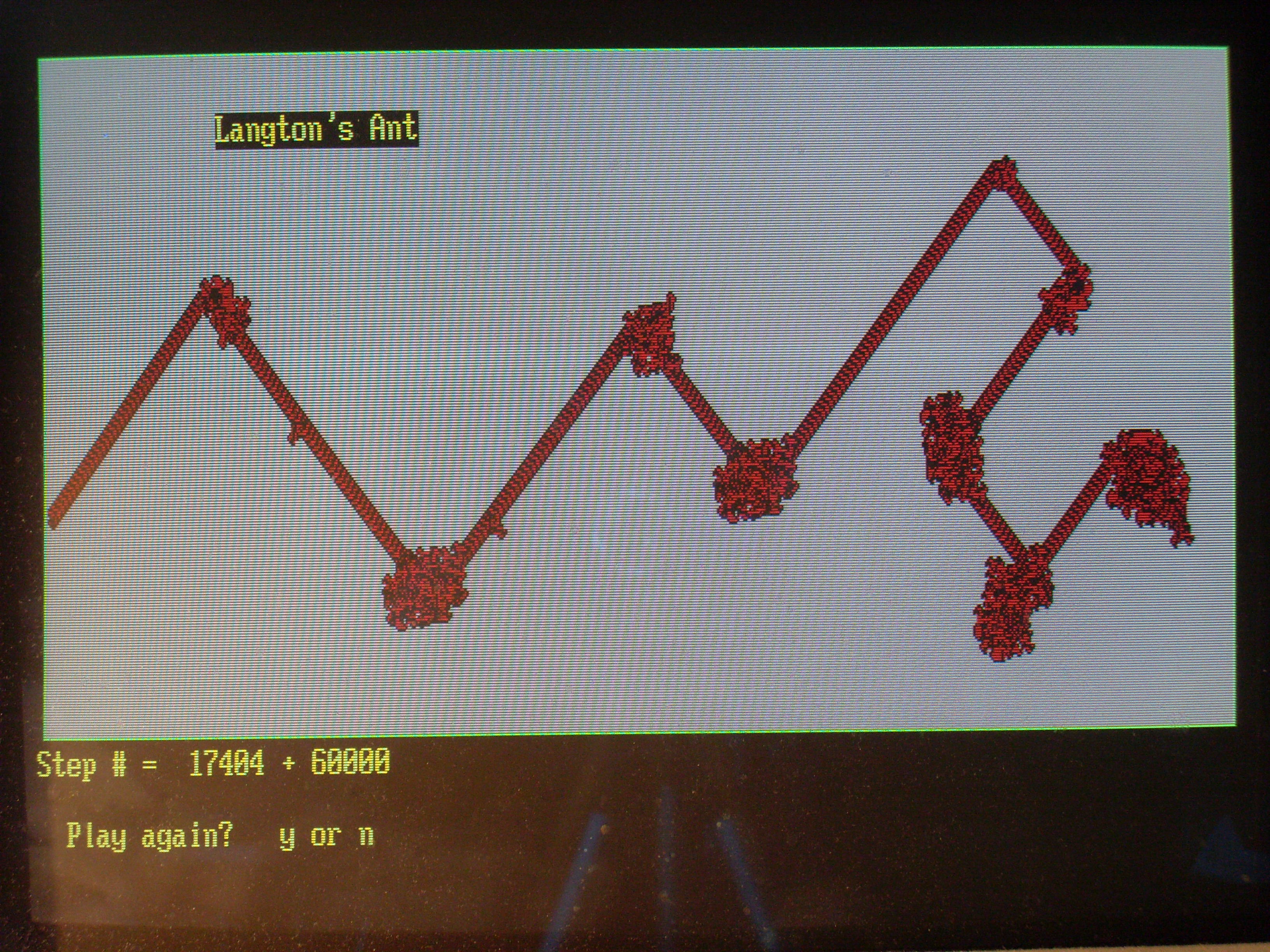
照片3:路径受到微扰的兰顿氏蚁行结果。
因为有些计算机不支持DOS编码程序,故我拍摄了视频短片来演示该程序运作过程。最近,经友人建议和帮助,又改用录屏技术,获得更清晰的视频,有兴趣的读者可以点击这里:MP4模式的视频链接:兰顿氏蚁行动态图,看看这隻受到微扰的兰顿氏蚁是如何转向,又如何不断地构建自己的“高速公路”。如有读者无法观看MP4模式,可试点击AVI模式的原摄影片视频链接。(片首的几秒钟是该程序的英文说明。如果手机或iPad不能正常显示该视频,可转到计算机上去看。)
这些运动对初始条件极其敏感的特点,表明按兰顿规则的蚁行是一个混沌的过程,它有一个平庸的“吸引子”(Attractor)。
混沌过程与无规则的随机过程,如微粒的布朗运动,有所不同。混沌过程看起来似乎也是杂乱无章,但它往往有明确的运动规则在内支配其行为,有些甚至可以用方程式来表述,它们统称为决定性系统(deterministic system)。但由于这些规则或方程对于初始条件极其敏感,或者系统对微扰的抗衡性极差,或者本身是强耦合的非线性动力学系统,例如,多体问题、复摆、湍流、相变及气象等过程,结果系统的行为“失之毫厘,谬以千里”,完全无法预测其在相空间的轨迹。虽然相空间的流线最终可能汇集在一个或几个有限的区域,其中许多不稳定的周期轨道与非周期轨道纠缠在一起,又相互排斥,形成所谓的“混沌吸引子”。
当然,兰顿氏蚁只是个简单而有趣的例子。一般而言,混沌现象中的“吸引子”,尤其是“奇异吸引子”(strange attractors)、从无序到有序的“自组织”(self-organization)和“自相似”(self-similarity),以及“原胞自动机”(cellular automata)的“自操作”(self-operation)和“自复制”(self-replication)等,都是些很迷人的现象和过程。现在人们认为,所谓远离平衡态的熵自发减少,与生命的起源有些联系。但为什么会是这样?熵为什么会自发减少?都是值得思考和研究的问题。兰顿的这篇论文就是想探究生命从无生气的人造“分子”的相互作用中形成的可能性。
80年代中,美国多数实验室还是用小型电子计算机(mini-computers),如PDP11,或Apollo DN660等工作站(work stations),软硬件与今日的微机难以相比,编程及显示都不容易。难得兰顿能想到用这么个简单的规则去穷追不捨,谁又能料得到,最后竟然发见有“自组织”的现象!这实在很令人佩服。后来的人,知道了结果,再重复并不难,难的是开路时的深思与执著。
[1]. Christopher. G. Langton, "Studying Artificial Life with Cellular Automata", Physica D 22, 120-149 (1986).
2017年8月
To read English version please click: Jim Shao, "Langton's Ants"
Or, goto http://www.azcolabs.com/xy_Langton_ant_Eng.html
参考阅读:
小鹰:《文革中我参加过的“相对论批判”》 (2018年6月)
小鹰:《争论的价值──犹太文化的启示》 (2020年8月) (附照片)
小鹰:《熵与状态》 (2023年10月17日)
小鹰:《闭卷判分 名人归零》 (2019年4月)