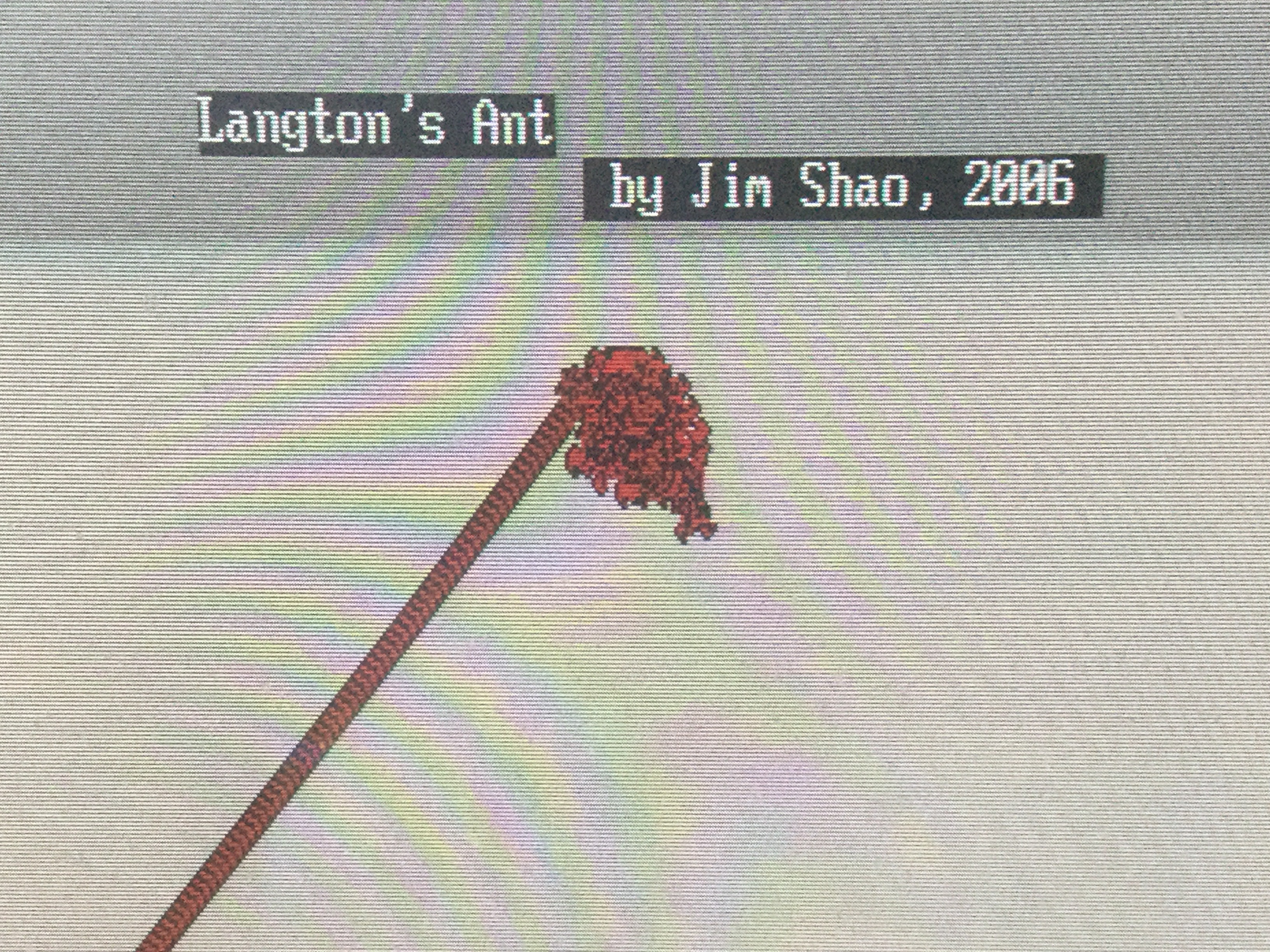
Photo 1: The trail of the ant under Langton's original conditions.
Jim Shao
Langton's ant is a two-dimensional, four-state Alan M. Turing machine created by Christopher Langton [1] in 1986.
The operating rules are as follows:
Place a virtual ant on an infinite chessboard with all white squares as background.
1, if the ant is at a black grid, the ant turns left 90 degrees into the adjacent grid;
2, if the ant is at a white (or red) grid, the ant turns right 90 degrees into the adjacent grid;
3, prior to entering the next grid, the ant should change its grid color from black to red or from white (or red) to black.
The result of continuous operation under these rules shows that after more than 10,000 steps of chaotic roaming, the ant finally begins to build a "highway" with a width of 104 steps (a periodic motion with drift), heading in a certain direction with unlimited extension until interference occurred.
In the year of 2006, out of curiosity and amusing myself, I repeated Langton's results by writing my own program according the above rules. (See photo 1).

Photo 1: The trail of the ant under Langton's original conditions.
Then I changed the initial conditions a bit, for example, pre-changing the background color of the grid next to the starting point. As a result, the ant's trail was very different from the previous one, though eventually it also built another "highway". (See photo 2).

Photo 2: The trail of Langton's ant with slightly changed initial conditions.
And then, again, I pre-alter randomly the background color of 10 grids on the route of the Langton's ant, trying to see how this ant would behave as he lost direction due to the interference? The results showed that, after each perturbations, sooner or later, the Langton's ant could always "stubbornly" rebuild its "highway", but the angle between the new road and the old road is either zero degree, or 70 degrees, or 110 degrees. (See photo 3).
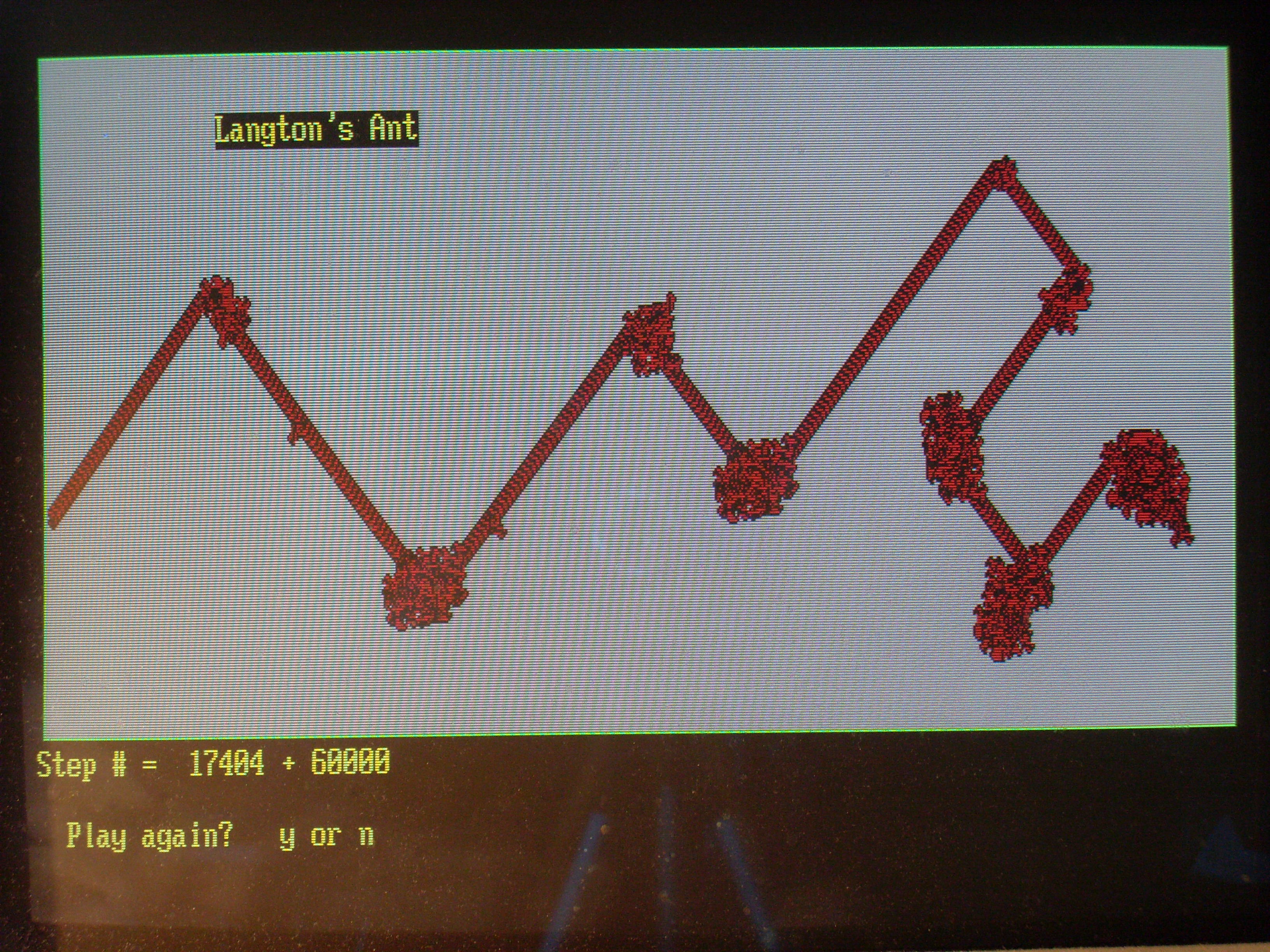
Photo 3: The trail of Langton's ant with 10 perturbations on its path.
Because some computers do not support the program running under DOS mode, I shot a video clip to demonstrate the operation of the program. Interested readers may click here: Video Link: Langton's Ants in Motion, or http://www.azcolabs.com/L_ant_vedio.mp4 to see how the disturbed ant is turning around and how to constantly rebuild their own "freeway". If readers are unable to watch MP4 mode, they can try clicking the video link on the original video in AVI mode: Video Link, or?http://www.azcolabs.com/L_ant_vedio.avi (The first a few seconds of the video is the English description of the program.) If the video can not be displayed normally on the iPhone or iPad, then try to watch it on a PC.
The extreme sensitivity of these motions to the initial conditions indicates that the movement of the Langton's ant is a chaotic process and it has a trivial "attractor" in the end.
Chaotic processes are different from random processes, such as Brownian particle irregular motion. The chaotic processes may seem disorderly too, but often they have explicit rules of movement governing their behaviors. Some may even be formulated as equations, which are collectively referred as the deterministic system. However, since these rules or equations are extremely sensitive to the initial conditions, or the systems are very poorly balanced against perturbation, or they are strongly coupled nonlinear dynamics systems, for example, multi-body problems, complex pendulum, turbulence, phase transition and meteorology. As a result, if the initial conditions are only missed slightest at the beginning, the behavior of the system ended up later with a thousand miles apart away. One can not predict its trajectory in phase space at all. Although the streamlines of phase space may eventually converge into one or a few finite areas, many of them are intertwined with non-periodic orbits and repel each other to form a so-called "chaotic or strange attractors".
Of course, Langton's ant is a simple and interesting example. In general, "strange attractors" and "cellular automata", "self-organization" and "self-similarity", "self-operation" and "self-replication" are all fascinating phenomena and processes often met in chaos.
Now people are thinking that the spontaneously reduced entropy at the state far away from the equilibrium might be related to the origin of life. But how this happens? Why entropy spontaneously decreases? It is worth while considering and researching those questions. Langton's thesis attempted to explore the possibility of life forming from the interaction of lifeless "molecules".
In the mid-1980s, most laboratories in the States were using mini-computers, such as PDP11, or Work Stations, like Apollo DN660, which were not very friendly to write programs or display graphics at that time. It is really admirable for Langton could think of using such simple rules, and finally found that there was a "self-organization" phenomenon in the end! Who could expect that? It is not too hard to repeat if knowing the result. It is difficult to have a deep thought and pursuing it persistently in the very beginning.
[1]. Christopher. G. Langton, "Studying Artificial Life with Cellular Automata", Physica D 22, 120-149 (1986).
August, 2017
Relevant Reading£º
Jim Shao£º"The three-body problem" (April 28, 2024)
Jim Shao£º"Entropy and State" (October 17, 2023)